行列をコレスキー分解をする|scilab入門
正定値対称行列を持つ連立一次方程式 Ax=b の場合にガウスの消去法の他にコレスキー分解を使用して解く場合があります。
行列Aが正定の場合, コレスキー分解は A=UU’となるような 上三角行列U、 またはU’ を出力します。
正定値対称行列とは
xAx’≧0
となるような行列です。
例として、任意の行列 A をコレスキー分解をして見ることにします。、
コレスキー分解:chol(行列)
ここであれば chol(A)
となります。
【計算をする】
A=[ 3 2 1; 2 3 2; 1 2 3];
U=chol(A)
–>A=[ 3 2 1; 2 3 2; 1 2 3];
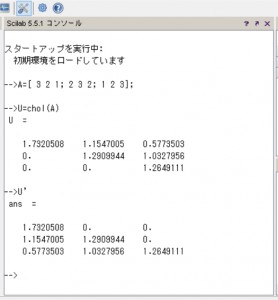
–>U=chol(A)
U =
1.7320508 1.1547005 0.5773503
0. 1.2909944 1.0327956
0. 0. 1.2649111
また、U’を表示する場合には、
U’
と入力をして enter を押してください。
このように表示されます。U と U’ を比較してみてください。Uの行とU’列が同じ値であることがわかります。転置行列となっています。
scilabによるUは上三角行列で。 U’ は下三角行列となります。
数学で表示すするUは下三角行列で
A =(下三角行列)(上三角行列)
となります。
コレスキー分解した行列をもとに戻す
さっき計算した行列を元に戻すには、
B=U’*U
のようにすると下の行列に戻ります。ここでは、戻した行列を B と置きました。
1. A=[ 3 2 1; 2 3 2; 1 2 3];
2. U=chol(A);
3. B=U’*U
–>A=[ 3 2 1; 2 3 2; 1 2 3];
–>U=chol(A);
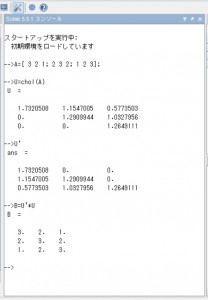
–>B=U’*U
B =
3. 2. 1.
2. 3. 2.
1. 2. 3.
このように戻ることが確認できると思います。
実行した画面は、次のようになります。
scilabでは元の行列は U’*U となり、また
U’*U と U*U’
で生成される行列は等しくありません。
関連記事
-

-
行列の対角要素を取り出す diag|scilab入門
行列の対角要素を取り出す場合には、diagを用います。 行列の対角要素や角線 …
-
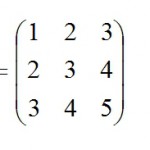
-
行列 3行3列の表示 |scilab入門
行列 Bが3行3列の場合 行列 が であるとします。これをscilabで表す場 …
-

-
行列の差の計算
行列の引き算についてです。 2つの行列の和について考えします。例として3行3列の …
-
-
2次元プロットにグリッドを追加:xgrid|グラフィック
グラフのデータを比較したいとか、見やすくしたい場合には、グリッドを入れて表示させ …
-

-
逆行列 inv|scilab入門
逆行列は、方程式を解くときに使います。 逆行列 inv を使用して解く場合につい …
-

-
行列に関係演算子を用いた計算とは|scilab入門
行列の要素ごとに関係演算子を適用して無ることにします。 次のような記号を関係演算 …
-

-
行列の積|scilab入門
今回は行列の積について実際に計算してみました。 簡単な計算でも実際計算してみない …
-
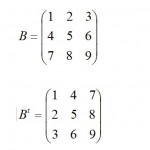
-
転置行列の表示 |scilab
転置行列の表示について 行列 Bの転置行列は、B にt を付けて表します。行の要 …
-

-
連立一次方程式を解いてみる|scilab入門
逆行列 inv と (¥)を用いて、簡単なの連立一次方程式を解いてみました。 次 …
-

-
行列の和の計算|scilab入門
行列の和の計算についてです。 2つの行列の和について考えます。例として3行3 …
- PREV
- 連立一次方程式を解いてみる|scilab入門
- NEXT
- 複素行列の作り方|scilab入門