3次元グラフィックス meshgridとmesh
2015/07/08
表示する場合には組み込み関数eshgrid, mesh をついで使用します。
それぞれの関数について簡単に説明します。
組込み関数 meshgrid
3次元グラフィックス表示に用いれられる組込み関数 meshgrid を用いて座標平面の格子点を計算します。
3次元のグラフを表示する場合には、次のようにします。
2つのベクトル行列
X=(x1,x2,…,xn)
Y=(y1,y2,…,yn)
を用い、組み込み関数meshgridを適用して座標平面の格子点からなる m × n 行の行列を作り出します。この格子座標を関数に代入して、3次元表示関数mesh等を用いて表示します。
組み込み関数mesh
行列を組み込み関数meshの引数として用いることによって、3次元のグラフを描くことができます。%epsはイプシロン (浮動小数点数相対精度)といい1+%eps=1となる最も大きい値で、零の割り算によるエラー回避に用います。
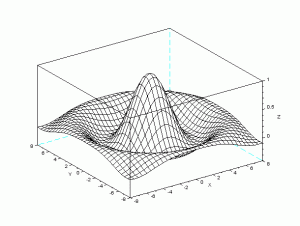
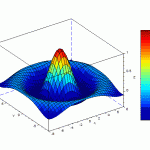
計算例:Z=sin(R)/R
例として次のような関数を計算してみることにします。
Z=sin(R)/R
R=SQRT(x^2+y^2)
を計算してみることにします
3次元表示:mesh
1. clf();
2. XI=-8:0.5:8;YI=XI;
3. [X Y]=meshgrid(XI,YI);
4. R=sqrt( X.^2 + Y.^2 ) + %eps;
5. Z=sin(R)./R;
6. mesh(X,Y,Z);
2行目はベクトル行列XI,YIを作成します。
範囲はxの範囲は -8 ~ 8.0 、yの範囲も-0.8 ~ 0.8 同様の範囲とします。
3行目はmeshgridで座標平面の格子点からなる 行の行列を作成します。
5行目は関数Z=sin(R)./Rの計算をします。
6行目はmesh(X,Y,Z)で3次元のグラフを表示します。
meshgrid と meshによる3次元表示をすることができました。関数を変えて違う図形を表示させてみて下さい。
関連記事
-
-
scilabのエディター SciNoteの使用
プログラムの作成に「SciNoteを起動」を使用するととても便利です。プログラム …
-
-
余りを求める modulo |scilab入門
除算をした場合に、余りを求めたい場合があります。 余りを求める関数がmodulo …
-
-
高速フーリエ変換 FFTの計算
高速フーリエ変換 FFT の計算を行ってみます。 フーリエ変換は雑音を含んだ …
-
-
グラフに文字列を描画 xstring
グラフに項目たタイトルの文字列を描画して見やすくする方法があります。 描画するグ …
-
-
べき乗 ^|scilab入門
べき乗の計算には ( ^ )を使います。 2の8乗についての計算は次のようになり …
-
-
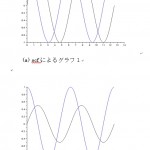
3次元曲面をカラープロット surf で表示する
3次元グラフィックスを表示する場合に surf を使用します。また、プロットした …
-
-
小数点以下切り捨て floor|scilab入門
小数点以下を切り捨てる場合に:floor を使います。 例として 1.523 …
-
-
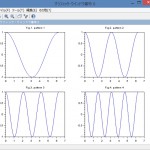
一つのグラフィックウインドウに複数のグラフを描くsubplot
一つのグラフィックウインドウに複数の裏婦を描き活用したい場合にとても便利なコマン …
-
-
円周率 π を表す|scilab入門
円周率 π を表す場合には、パーセントの後にpiとし %pi のように表記しま …
-
-
複数のグラフィック・ウィンドウを開く scf
グラフを重ね書きをしないで、表示させたい場合に scf を用いるととても便利です …