3次スプライン補間 splin について!
2015/05/27
計測したデータを補間して表示させたい場合には、3次スプライン補間 splinを用いると見やすくなります。離散的なデータをフラットな曲線で表示できるので、データの推移を把握できます。
splin関数は3次スプライン補間で
d = splin(x, y ,spline_typ)
のようになります。この関数は、点(xi,yi)を補間し、i=1,..,nについてs(xi)=yi となる3次スプラインで補間します。また、spline_typeパラメータにより、いくつかの種類のスプラインを利用することができます。
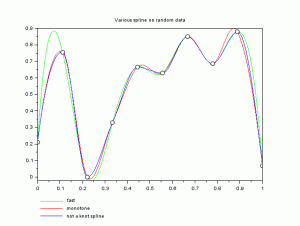
例として、補間の区間は[0,1]、データの個数は10個、データは乱数で作成し、スプラインの評価点は800点として、3次スプライン補間を行なってみることにします。
次のようなプログラムを実行すると得ることができます。
1. //異なるスプラインの計算
2. a = 0; b = 1; // 補間の区間
3. n = 10; // 補間点の個数nb
4. m = 800; // 評価を行う離散点
5. x = linspace(a,b,n)’; // 補間点の横座標
6. y = rand(x); // 補間点の縦座標
7. xx = linspace(a,b,m)’;
8. yk = interp(xx, x, y, splin(x,y,”not_a_knot”)); //デフォルト
9. yf = interp(xx, x, y, splin(x,y,”fast”)); //ローカルなスキーム
10. ym = interp(xx, x, y, splin(x,y,”monotone”));//単調なスキーム
11. clf()
12. plot2d(xx, [yk yf ym ], style=[3 5 2 ], strf=”121″, …
13. leg=”fast@monotone@not a knot spline”)
14. plot2d(x,y,-9, strf=”000″) // to show interpolation points
15. xtitle(“Various spline on random data”)
16. show_window()
5行目は補間する座標点の計算で、区間[0,1]を10等分します。
6行目は乱数でデータを10個作成しています。7行目は区間[0,1]を離散評価点800点としています。
8行目は3次スプラインがデフォルトで計算されます。計算結果をykとしています。
9行目は3次スプラインがローカルなスキームで計算されます。計算結果をyfとしています。
10行目は3次スプラインが区間で単調となるようなスキームで計算されます。計算結果をymとしています。
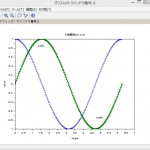
12行の継続行が13行目です。ここでは、異なる3次スプラインの結果を表示します。3次スプラインyk=”not_a_knot”、yf =”fast”、ym =”monotone”の順で、線の色はそれぞれ、緑、赤、青となっています。
14行目は元のデータを○(-9)で表示しています。
15行目はグラフのタイトルを表示しています。
16行目はカレントのグラフィックウインドウを前面に出します。
この結果からすると3次スプライン補間を行う場合には、ローカルなスキームで計算される”fast”か、単調となるようなスキームで計算される”monotone”がごく自然で適しているようです。
関連記事
-
-
複数の色を用いてグラフを描く plot2d
ヒトツノウインドウにラインの色を変化させて、数個のグラフを重ねて表示することにし …
-

-
行列の成分を取り出す tril|scilab入門
行列の成分を取り出す場合には、diag、tril、triuを用います。 ・dia …
-
-
ポリゴンを任意の色で塗りつぶす xfpoly
ポリゴンを塗りつぶしたい場合があるかと思いっます。 塗りつぶす命令として xfp …
-
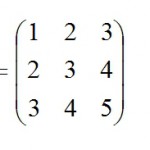
-
行列 3行3列の表示 |scilab入門
行列 Bが3行3列の場合 行列 が であるとします。これをscilabで表す場 …
-
-
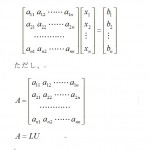
LU分解法で方程式を解く
方程式を LU分解法 (decomposition) で解くことにします。 元連 …
-
-
グラフに文字列を描画 xstring
グラフに項目たタイトルの文字列を描画して見やすくする方法があります。 描画するグ …
-
-
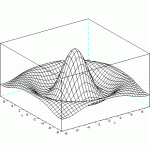
3次元グラフィックス meshgridとmesh
表示する場合には組み込み関数eshgrid, mesh をついで使用します。 そ …
-

-
行列の対角要素を取り出す diag|scilab入門
行列の対角要素を取り出す場合には、diagを用います。 行列の対角要素や角線 …
-

-
行列の差の計算
行列の引き算についてです。 2つの行列の和について考えします。例として3行3列の …
-
-
ifによる分岐と関係演算子・論理演算子
繰り返し処理に if による分岐と関係演算子・論理演算子 を用いることにします。 …
- PREV
- 3次元曲面をカラープロット surf で表示する
- NEXT
- 高速フーリエ変換 FFTの計算