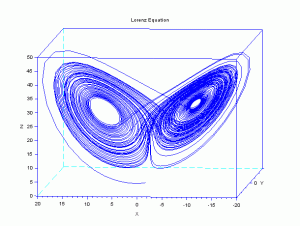
ローレンツモデルのカオス
ローレンツモデルのカオスを計算してみました。
Lorenzモデルは上下に温度差のある流体の運動が温度差によって対流から乱流に移流する状態を記述する運動方程式で、下記の式で表されます。
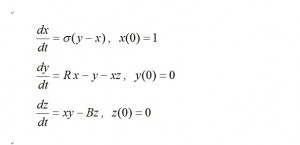
変数x, y, z は速度場、温度場、および平均の対流速度に比例する規格化された量です。σ、 R、 B はPrasel数,Rayleigh数、波数を示す定数である。
σ をs=10.0、R をr=28、B をb= 8/3とし、時間tを0から80とし、時間ステップ幅を0.02(s)として計算することにします。
1.ローレンツモデル計算
以下のようなプログラムを実行すると得られます。
1. // subroutine サブプログラム
2. function xdot=fun(t,x)
3. s=10.0;
4. r=28.0;
5. b=8/3;
6. xdot(1)=s*(x(2)-x(1));
7. xdot(2)=r*x(1)-x(2)-x(1)*x(3);
8. xdot(3)=-b*x(3)+x(1)*x(2);
9. endfunction
10. //mainプログラム
11. ta=0;tstep=0.02;tb=80;t0=0;
12. t=ta:tstep:tb;
13. // exec(‘c:\scilab_data\fun.sce’,-1);//ロード
14. // exists(‘fun’)
15. xx=ode([1;0;0], t0,t,fun);
16. clf();
17. xset(‘color’,2);//青色で
18. param3d(xx(1,:),xx(2,:),xx(3,:),95,80,’X@Y@Z’); //x y z
19. xtitle(“Lorenz Equation”);
2.プログラムの概略
6行目は1番目の式です。
7行目は2番目の式です。
8行目は3番目の式です。
11行目はステップ時間と、計算時間です。ステップは0.02〈s〉で、時間は80(S)です。
12行目は時間tの行列を作成しています。
15行目では関数odeを呼び出して計算をしています。
16行目でグラフィックウィンドウをクリアにしています。
17行目でカラーの指定です。
18行は計算結果を3次元表示します。
19行目はグラフにタイトルを付けています。
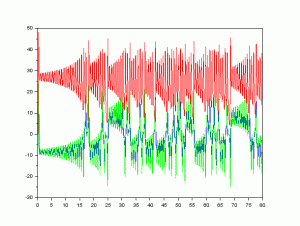
3.ローレンツモデルのカオスの時間に対する振幅
ローレンツモデルの時間に対する振幅を示すと図のようになります。
上のプログラムを実行した後、次のようなプログラムを実行すると得られます。
1. clf();
2. plot(t,xx(1,:),’b’,t,xx(2,:),’g’,t,xx(3,:),’r’)
function を使用するとちょっとしたプログラムを作成できます。
レスラーモデルも同様な方法で計算できますので、計算してみて下さい。
訪問あるがとうございます。また来てください。
関連記事
-
-
カオスと微分方程式 ロジスティック曲線
カオスと微分方程式についてです。 カオス ( Chaos) とは、「混沌」という …
-
-
関数のオンライン定義 deff を使ってみる!
関数のオンライン定義を用いると、数式だけを呼び出して計算ができます。 関数 fu …
- PREV
- カオスと微分方程式 ロジスティック曲線
- NEXT
- 多項式を用いた線形システムの定義 syslin