組み込み関数functionによる計算
2015/06/23
組み込み関数 function を使用してファン・デル・ポール方程式を計算することにします。
微分方程式ソルバを用いてプログラムよりもステップ数が多くなりますが、
数式に沿ったプログラムになるのであとで見た場合も見やすいような気がします。
ファン・デル・ポール方程式をfunction関数を用いて解くことにします。functionを用いた場合のプログラムを以下に示しました。組み込み関数functionを用いて記述されたプログラムを保存して、保存先フォルダから読み込んで計算することもできます。
ここでは、保存せずに一緒に記述した状態で実行することにします。
・functionによるプログラム
1. // sub – program file name :rlc.sce
2. function [ydot]=rlc(t,y)
3. myu=1.0;
4. dy1=y(2);
5. dy2=myu*(1-y(1)^2)*y(2)-y(1);
6. ydot=[dy1;dy2];
7. endfunction
8. // main – program
9. t=0:0.1:20;
10. y0=[1;0.25];
11. t0=0;
12. //exec(‘c:\scilab_data\rlc.sce’,-1);// rlc.sciファイルをロード
13. exists(‘rlc’)
14. y=ode(y0, t0,t,rlc);
15. clf();
16. //xset(‘color’,2);//青色
17. plot(t,y);
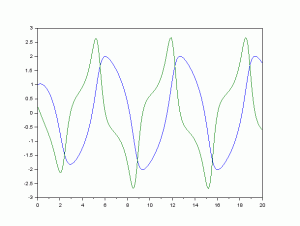
上記のプログラムを実行すると、次のような図が得られます。
プログラの詳細は、ソルバを使用した微分方程式の解法 を参考にしてください。
大きなプログラムを作成する場合には、function を利用すると便利です。
関連記事
-
-
ソルバを使用した微分方程式の解法
Silabは微分方程式を解くための微分方程式ソルバが用意されています。そこで、ソ …
-
-
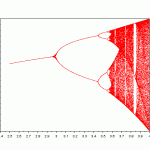
カオスと微分方程式 ロジスティック曲線
カオスと微分方程式についてです。 カオス ( Chaos) とは、「混沌」という …
- PREV
- ソルバを使用した微分方程式の解法
- NEXT
- 平均値と標準偏差