行列に関係演算子を用いた計算とは|scilab入門
行列の要素ごとに関係演算子を適用して無ることにします。
次のような記号を関係演算子といいます。
>=:より大きか等しい(以上)
>:より大きい
=<:より小さいか等しい(以下)
<:より小さい
==:等しい
~=ひとしくない
行列の成分についても関係演算子を適用することができます。
(1) 行列の要素が等しい場合:Cequal
行列の要素が等しい場合に真として ” T ”を返し、偽の場合にはfaluseとして “ F ”を返します。
A=[ 3 1 5 2 7 ]
B=[ 3 2 5 4 1 ]
Cequal=(A==B)
->A=[ 3 1 5 2 7 ]
A =
3. 1. 5. 2. 7.
–>B=[ 3 2 5 4 1 ]
B =
3. 2. 5. 4. 1.
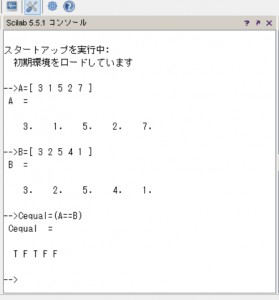
–>Cequal=(A==B)
Cequal =
T F T F F
行列の要素が等しい場合はTが、等しくない場合はFが表示されます。
(2) 行列の要素が等しくない場合:Cnotequal
A=[ 3 1 5 2 7 ]
B=[ 3 2 5 4 1 ]
Cnotequal=(A ~= B)
–>A=[ 3 1 5 2 7 ]
A =
3. 1. 5. 2. 7.
–>B=[ 3 2 5 4 1 ]
B =
3. 2. 5. 4. 1.
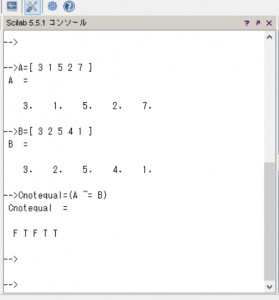
–>Cnotequal=(A ~= B)
Cnotequal =
F T F T T
行列の要素が等しい場合はF、等しくない場合はTが表示されます。
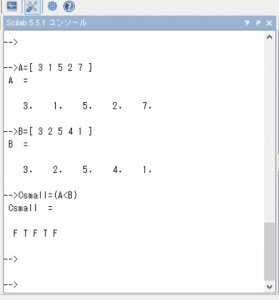
(3) Aの要素がBの要素より小さい:Csmall
A=[ 3 1 5 2 7 ]
B=[ 3 2 5 4 1 ]
Csmall=(A
A =
3. 1. 5. 2. 7.
–>B=[ 3 2 5 4 1 ]
B =
3. 2. 5. 4. 1.
–>Csmall=(A< B)
Csmall =
F T F T F
行列の要素が大きい場合はT、小さい要素はFが表示されます。
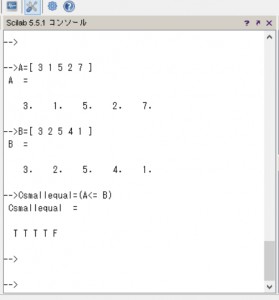
(4) A要素がBの要素以下の場合:Csmallequal
A=[ 3 1 5 2 7 ]
B=[ 3 2 5 4 1 ]
Csmallequal=(A<= B)
-->A=[ 3 1 5 2 7 ]
A =
3. 1. 5. 2. 7.
–>B=[ 3 2 5 4 1 ]
B =
3. 2. 5. 4. 1.
–>Csmallequal=(A<= B)
Csmallequal =
T T T T F
行列Aの要素がBの要素以下の場合には“T”が表示さ、そうでないならば“F”が表示されます。
(5) A要素がBの要素より大きい場合:Clarge
A要素がBの要素より大きい場合“T”
A=[ 3 1 5 2 7 ]
B=[ 3 2 5 4 1 ]
Clarge=(A> B)
–>A=[ 3 1 5 2 7 ]
A =
3. 1. 5. 2. 7.
–>B=[ 3 2 5 4 1 ]
B =
3. 2. 5. 4. 1.
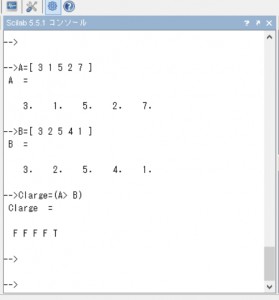
–>Clarge=(A> B)
Clarge =
F F F F T
行列Aの要素が行列Bの要素より大きい場合“T”が表示、そうでないならば“F”が表示されます。
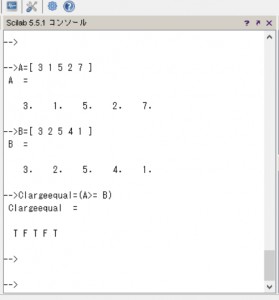
(6) A要素がBの要素以上の場合:Clargeequal
A=[ 3 1 5 2 7 ]
B=[ 3 2 5 4 1 ]
Clargeequal=(A>= B)
–>A=[ 3 1 5 2 7 ]
A =
3. 1. 5. 2. 7.
–>B=[ 3 2 5 4 1 ]
B =
3. 2. 5. 4. 1.
–>Clargeequal=(A>= B)
Clargeequal =
T F T F T
行列Aの要素が行列Bの要素以上の場合には“T”が表示され、そうでないならば“F”が表示されます。
関連記事
-

-
行列の和の計算|scilab入門
行列の和の計算についてです。 2つの行列の和について考えます。例として3行3 …
-

-
行列の積|scilab入門
今回は行列の積について実際に計算してみました。 簡単な計算でも実際計算してみない …
-
-
複数の色を用いてグラフを描く plot2d
ヒトツノウインドウにラインの色を変化させて、数個のグラフを重ねて表示することにし …
-
-
whileによる繰り返し処理
繰り返し処理 for の他に、whileを使用した繰り返し処理の計算方法がありま …
-

-
行列の成分を取り出す tril|scilab入門
行列の成分を取り出す場合には、diag、tril、triuを用います。 ・dia …
-

-
行列の差の計算
行列の引き算についてです。 2つの行列の和について考えします。例として3行3列の …
-
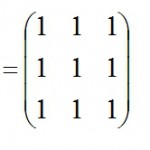
-
ゼロ行列や定数行列を作る |scilab入門
ゼロ行列や定数行列を作ることにします。 ゼロ行列:zeros 定数行列:on …
-
-
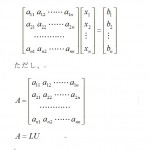
LU分解法で方程式を解く
方程式を LU分解法 (decomposition) で解くことにします。 元連 …
-
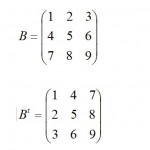
-
転置行列の表示 |scilab
転置行列の表示について 行列 Bの転置行列は、B にt を付けて表します。行の要 …
-
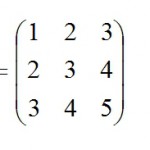
-
行列 3行3列の表示 |scilab入門
行列 Bが3行3列の場合 行列 が であるとします。これをscilabで表す場 …