高速フーリエ変換 FFTの計算

高速フーリエ変換 FFT の計算を行ってみます。

　フーリエ変換は雑音を含んだ N 個の離散データ からなる信号 x,x2,…,xn のなかからある周波数成分 Xを見つけるために用いられます。また、 X から x を求めることを逆変換といいます。

　X を効率よく計算するアルゴリズムが高速フーリエ変換（Fast Fourier Transform; FFT）と呼ばれています。scilabを用いて FFT 解析を行ってみることにします。

例として、サンプリング周波数を１kHzとし、周波数が50,90Hzの合成波のノイズがないものとして周波数を求めてみることにします。以下のようなプログラムを実行することによって得られます。


(1) ノイズなしの場合のFFT解析

1. // pure frequencies : 50 and 90 Hz
2. sample_rate=1000;
3. t = 0:1/sample_rate:0.5;
4. N=size(t,’*’); //number of samples（501）
5. clf();
6. s=sin(2*%pi*50*t)+sin(2*%pi*90*t+%pi/4);//+grand(1,N,’nor’,0,2);
7. subplot(2,1,1)
8. plot(t,s)
9. y=fft(s);
10. f=sample_rate*(0:(N/2))/N; //associated frequency vector
11. n=size(f,’*’)
12. subplot(2,1,2)
13. plot(f,abs(y(1:n)))


【プログラムの主なな概要】
2行目ではサンプリング周波数1000Hzとします。
3行目ではサンプリング時間を0.5(s)で時間ステップは0.001(s)です。
4行目ではサンプリング数で501個となります。
6行目でノイズがない場合の50,90Hzの合成波を求めています。
7行目でサブウインドウを指定しています。
8行目では合成波を表示しています。
9行目ではFFTの計算を行っています。
10行目で周波数を求めています。
11行ではサブウインドウを指定しています。
12行目ではfを横軸にFFTの値を表示します。

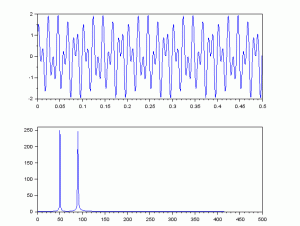
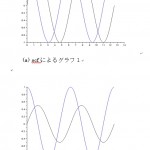
上の波形は、解析するための波形で、下の図はFFT解析による図です。
図からわかるように50Hz,と90Hzの波形のピーク値が見られます。周波数が混在した波形から、その波形が構成されている周波数を推測できます。
周波数解析においてFFTは、有効な手法の一つであることがわかります。