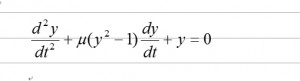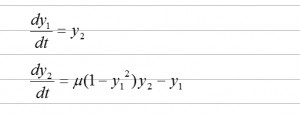ソルバを使用した微分方程式の解法
2015/06/16
Silabは微分方程式を解くための微分方程式ソルバが用意されています。そこで、ソルバを使用して微分方程式を解いてみることにします。
微分方程式については、数学の参考書にしてください。私たちが一般的に取り扱うのは、常微分方程式です。
有限要素法はこの常微分方程式を離散化することによって計算されています。
微分方程式ソルバ:ode
例として、ファン・デル・ポール方程式を解いてみることにします。エサキダイオードの発振回路の発振波形を表示することにします。
ただし、 ηは定数である。
方程式が高階導関数の場合には、高階導関数を別の変数に置き換えて一階の微分方程式にします。ここで、 η を定数とし y1=t , y2=dy2/dt とすると方程式は、
となり、2変数の1階微分方程式となります。
Scilabの微分方程式ソルバは
y=ode(y0,t0,t,f)
のようになります。また、パラメータは次のようになっています。
y0:初期条件の実数ベクトル
t0:初期時間の実数スカラー
t:解を計算するための時間で実数ベクトル
f:関数type
微分方程式ソルバを用いて、次のようなプログラムを実行してファン・デル・ポール方程式を解いてみることにします。
プログラム例
1. clf();
2. deff(‘[ydot]=f(t,y)’,[‘myu=1;’,’dy1=y(2);’,…
3. ‘dy2=myu*(1-y(1)^2)*y(2)-y(1);’,…
4. ‘ydot=[dy1;dy2];’]);
5. t=0:0.1:20;
6. y0=[1;0.25];
7. t0=0;
8. y=ode(y0, t0,t,f);
9. plot(t,y)
プログラムの説明
2~4行は継続行です。長くなると分かりづらいのでこの容器記述しています。見やすい事と間違いを少なくするためです。
5行目は計算時間とステップ時間です。
6行目は初期条件です。
8行目でソルバによる計算です。
ファン・デル・ポール方程式を解いて、表示させると図のようになります。ファン・デル・ポール方程式は、非線形の例題としてよく取り上げられます。
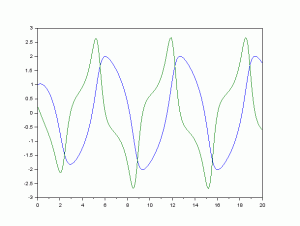
手直しをしてファン・デル・ポール位相面も画いてみてください。いろいろな角度から見ることによって考察を広げることができます。
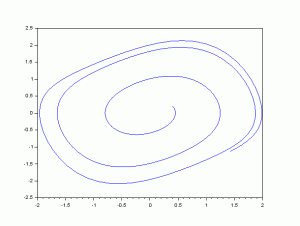
描くことができましたか?
位相メン図を描く場合には、時間 t とは無関係に計算した結果を用いて表示させると良いです。
関連記事
-
-
カオスと微分方程式 ロジスティック曲線
カオスと微分方程式についてです。 カオス ( Chaos) とは、「混沌」という …
-
-
組み込み関数functionによる計算
組み込み関数 function を使用してファン・デル・ポール方程式を計算するこ …
- PREV
- 多項式が有利式の場合の計算
- NEXT
- 組み込み関数functionによる計算