線形システムと多項式行列 syslin

線形システムの状態空間表現の多項式行列　：syslinの使い方について。


システム方程式が線形の場合には線形時不変(linear time varying system)となり

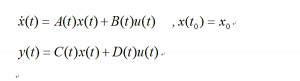
と表されます。
ただし、 A(t)：システム行列、 B(t)：入力行列、C(t) ：出力行列、 D(t)：直達行列、
x(t) 状態変数ベクトル、u(t) 入力変数ベクトル、y(t) 　出力変数ベクトルである・


システム係数行列（system coefficient matrix） A(t),B(t),C(t),D(t)が，時不変の場合には線形時不変(linear time-invariant system)と呼ばれ





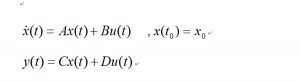
と表されます。ここで、A,B,C,D の係数行列は定数行列です。

多項式行列　：syslin
線形システムはsyslinを用いて定義します。


[sl]=syslin(dom,A,B,C [,D [,x0] ])


A,B,C,Dは状態空間表現の行列です。 (D はオプションで,デフォルトでは ゼロ行列となります)。プロパーでないシステムでは,D は多項式行列となります。
x0はベクトル (初期状態量; デフォルト値は 0)です。
syslin はリストとして線形システムを定義して, データの整合性を行います。ここで、
dom はシステムの時間領域を指定で,連続時間システムの場合dom=’c’, 離散時間システムの場合 dom=’d’ です。

【プログラム】

1.s=poly(0,’s’)
2.H=(1+2*s)/(2+3*s+s^2)
3.S1=syslin(‘c’,H)

【実行結果】
–>H=(1+2*s)/(2+3*s+s^2)
H =

1 + 2s
———-
　　　　　　　　 2
2 + 3s + s

–>S1=syslin(‘c’,H)
S1 =

1 + 2s
———-
　　　　　　　　2
2 + 3s + s


多項式の線形システムの状態空間表現となります。

【２．線形システムを定義】


1.s=poly(0,’s’);
2.A=[0,1;0,0];B=[1;1];C=[1,1];
3.S1=syslin(‘c’,A,B,C) //線形システムを定義


【実行結果】

–>S1=syslin(‘c’,A,B,C) //線形システムを定義
S1 =

S1(1) (state-space system:)

!lss A B C D X0 dt !

S1(2) = A matrix =

0. 1.
0. 0.

S1(3) = B matrix =

1.
1.

S1(4) = C matrix =

1. 1.

S1(5) = D matrix =

0.

S1(6) = X0 (initial state) =

0.
0.

S1(7) = Time domain =

c


行列A,B,C,D,X0(初期値),時間領域を表示します。

線形システムはsyslinを用いて定義します。
A,B,C,Dは状態空間表現の行列です。
ボード線図を表示するときには、syslinを用います。