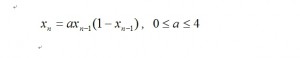カオスと微分方程式ロジスティック曲線

2015/07/03

カオスと微分方程式についてです。
カオス ( Chaos) とは、「混沌」という意味です。

物理現象を表す場合には、微分方程式で表します。この微分方程式が安定しないで、振動をする場合をカオス現象と呼んでいます。
詳細は他書を参考にしてください。

ロジスティック
ロジスティック曲線を解く場合には、式のような差分方程式にして直して解きますが、このaの値によってカオス現象がみられます。

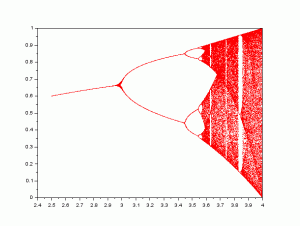
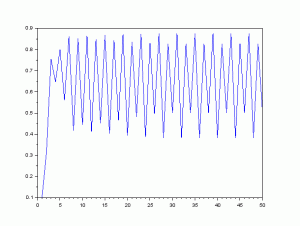
ここで、a=2.5 、x=0.1 として計算をすることにします。このときの値をy軸に、反復回数n をx横軸にとると図のようになります。

最初に小さな過渡状態から安定になります。次のようなプログラムを実行すると得ることができます。また、a の値を a=3.5にすると振動するここが分かります。

SPONSORED LINK

ex-011-001
1. n=50;a=2.5;
2. x=zeros(n,1);
3. x1=0.1;
4. x(1)=x1;
5. for i=2:n
6. x(i)=a*x(i-1)*(1-x(i-1));
7. end
8. t=[1:n];
9. clf();
10. plot(t,x)

計算すると図のようなグラフが表示されます。

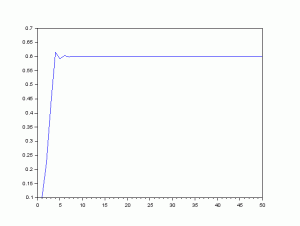
a=3.5とすると図のようになります。

次にパラメータの値を細かく変化させて調べてみることにします。パラメータ aを横軸xにとり縦軸yにx をとりプロットすると3.5≦a≦4.0 の間で分岐しているのが分かります。次のようなプログラムを実行すると得ることができます。

ex-011-003
1. nmax = 200;
2. nout = 80;
3. A = [2.5:0.001:4];
4. X = 0.8 * ones(nmax,length(A));
5. for n = 1: nmax – 1
6. X(n+1,:) = A .* X(n,:) .* (1.0 – X(n,:));
7. end
8. clf();
9. plot(A,X(nout:nmax,:),’.r’,’markersize’,1);

実行すると以下のような。図が表示されます。

いろいろな現象を計算してみて下さい。
思わぬことに気づくかもしれません。
シュミレーションは誰がやっても同じ結果が出なければいけません。

同じ方程式で、同一条件を使用したなら必ず同じ結果が得られるはずです。
再現性を確実にして、初めて貴重な資料が作成できます。

訪問ありがとうございました。
またのご訪問をお待ちしています。

次回は、ローレンツモデルのカオスです。