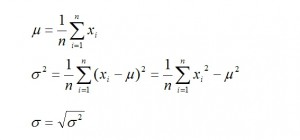平均値と標準偏差

統計の処理をする場合には、平均値や標準偏差のを求める時が多々あると思います。


そこで、データの平均値と標準偏差やデータのソート、正規分布、最小二乗法による直線近似を行うことにします。


1。　平均値と標準偏差
個のデータ があったとする。この平均値 、標準偏差 、分散 は

。
のように表される。ただし、データの個数が少ない場合には

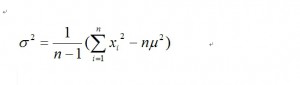
として計算をすします。データの個数が２０個とかの場合に使用します。

計算例
例として、データ68, 72, 74, 61, 50, 80, 40, 70, 65, 81.の平均値 、標準偏差 、分散 を求めるプログラムを作成することにします。ここでは、次のようなプログラムを実行することにします。

1. x=[68 72 74 61 50 80 40 70 65 81] ;//データ
2. n=10; //データの個数
3. s=sum(x)
4. m=mean(x)
5. v2=(sum(x.^2)-n*m^2 )/(n-1)
6. v=sqrt(v2) //計算標準偏差
7. stdev(x) //組み込み標準偏差

–>s=sum(x)
s =
661.
–>m=mean(x)
m =
66.1
–>v2=(sum(x.^2)-n*m^2 )/(n-1)
v2 =
166.54444
–>v=sqrt(v2) //計算標準偏差
v =
12.90521
–>stdev(x) //組み込み標準偏差
ans =
12.90521

データの合計が661、平均66.1、 分散は 166.54444 、標準偏差は12.0952 のようになります。
mean:平均値の計算
stdev：組み込み標準偏差

2. データのソート:gsort
データソートには降順、昇順、配列のソート等があります。


[b,k]=gsort(a,option,direction)
のようにして使用します。ここで、aは実数か整数または文字列のベクトル行列です。
Optionで’r’を指定するとa の各列のソート、’g’:を指定すると行列の全要素のソート、’c’を指定するとの各行のソート、’lr’を指定すると列の辞書式ソート、’lc’を指定すると行の辞書式ソートをします。


directionで文字列の ソートの方向を指定します。 ‘i’ は昇順, ‘d’ は降順 (デフォルト)を意味します。また、bはaと同じ型と次元の配列で、kは整数値を有し行れるaと同じ次元の実数配列で元の添え字を有します。

// 各列のソート, ‘i’ は昇順,
1. a=[ 2 3 4 6 1 5]
2. [ a1,k]=gsort(a,’r’,’i’)
–>a=[ 2 3 4 6 1 5]
a =
2. 3. 4. 6. 1. 5.
–>[ a1,k]=gsort(a,’r’,’i’)
k =
1. 1. 1. 1. 1. 1.
a1 =
2. 3. 4. 6. 1. 5.

この行列は１行６列の行列なので、１列目には２だけです、同様に２列目は３、３列目は４，４列目は６，５列目は１，６列目は５です。
行列がそのまま、表示されることになります。

ご訪問ありがとうございます。
またお越し下さい。